 Mathematik ist zwar unter anderem eine wichtige Sprache für Formulierungen innerhalb der (Natur-)Wissenschaften, als solche selbst jedoch eine Strukturwissenschaft. Es werden also scheinbar keine Theorien mit konkreten Vorhersagen über die Wirklichkeit aufgestellt, die man dann versucht experimentell zu widerlegen und als wahrscheinlich richtig ansieht wenn die Widerlegung immer scheitert (die Vorhersagen also stimmen), stattdessen werden aus wenigen grundlegenden Axiomen logische Schlüsse gezogen, die sich innerhalb dieses Sytems tatsächlich beweisen (nicht nur nicht widerlegen) lassen und damit dort dann wahr sind.
Mathematik ist zwar unter anderem eine wichtige Sprache für Formulierungen innerhalb der (Natur-)Wissenschaften, als solche selbst jedoch eine Strukturwissenschaft. Es werden also scheinbar keine Theorien mit konkreten Vorhersagen über die Wirklichkeit aufgestellt, die man dann versucht experimentell zu widerlegen und als wahrscheinlich richtig ansieht wenn die Widerlegung immer scheitert (die Vorhersagen also stimmen), stattdessen werden aus wenigen grundlegenden Axiomen logische Schlüsse gezogen, die sich innerhalb dieses Sytems tatsächlich beweisen (nicht nur nicht widerlegen) lassen und damit dort dann wahr sind.
Somit drängt sich die Frage (die ich schon hier gestellt habe) auf, ob die Mathematik eine Erfindung von uns Menschen oder eine dem Universum inhärente Wahrheit ist, die wir (und zumindest implizit auch andere Lebewesen) entdecken.
Im Grunde geht es bei dieser Frage um die Axiome, aus denen der Rest hergeleitet wird, wie z.B. „Jede natürliche Zahl n hat genau einen Nachfolger n‘.“ aus der Peano-Arithmetik. Wenn man solche Dinge aus in uns intuitiv vorhandenen Regeln der Mengenlehre extrahiert, reduziert sich das Problem darauf, wo diese Intuition herkommt. Aber zunächst einmal: Wie sieht sie aus? Unser physikalisches Universum scheint (zumindest auf makroskopischer Ebene) die Eigenschaft zu haben, diskrete Objekte beinhalten zu können. Wenn alles einfach nur Suppe wäre, würden wir vermutlich (zumindest wenn wir als Grundannahme setzen, dass wir tatsächlich existieren und unsere Sinne zumindest manchmal sinnvolle Daten liefern, ansonsten sind wir eh einfach nur raus) nicht die Vorstellung von einzelnen (zusammenzählbaren usw.) Objekten entwickeln.
 Aus diesen Mengen ergibt sich dann, was wir mit ihnen tun können:
Aus diesen Mengen ergibt sich dann, was wir mit ihnen tun können:
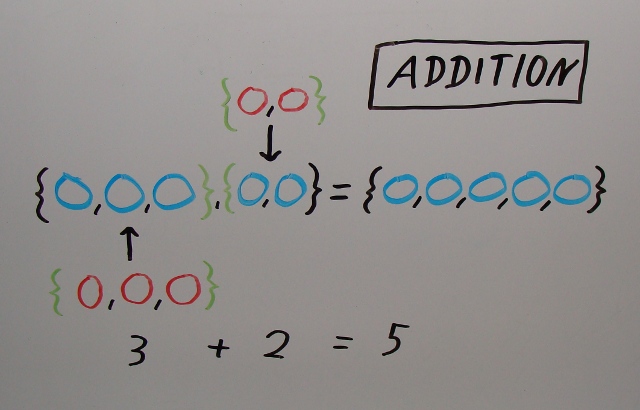 usw. mit den anderen Operationen, die auch andere Sachen machen, als mit der Mächtigkeit von Listen zu operieren. (Mehr dazu hier: http://www.youtube.com/watch?v=14JavH4Rk7k#t=8m20s) Der schlaue David sagt übrigens, dass sich aus der rekursiven Definition der Addition (a+0 = a, a + b‘ = (a+b)‘), ergibt, dass das n‘ von oben (also der Nachfolger von n) dann n+1 ist. 😉
usw. mit den anderen Operationen, die auch andere Sachen machen, als mit der Mächtigkeit von Listen zu operieren. (Mehr dazu hier: http://www.youtube.com/watch?v=14JavH4Rk7k#t=8m20s) Der schlaue David sagt übrigens, dass sich aus der rekursiven Definition der Addition (a+0 = a, a + b‘ = (a+b)‘), ergibt, dass das n‘ von oben (also der Nachfolger von n) dann n+1 ist. 😉
Wenn wir mathematisch rumhantieren, vergessen wir nur gerne mal, dass all diese Grundvorstellungen in den verschiedendsten Kulturen von Generation zu Generation gleichermaßen entstehen (es wäre mal witzig, zu erfahren, ob Außerirdische auf die gleichen Dinge kämen), weil sie einfach jeder persönlich täglich empirisch implizit anwendet und somit quasi ständig überprüft. Wenn zwei Äpfel und drei Bananen nicht immer sondern nur manchmal fünf Öbste ergeben würden, sollte das doch irgendwann mal auffallen, oder? 😉 Im Prinzip ist Addition also eine Theorie über das Verhalten der Natur.
Logik, die wir benutzen, um aus solchen Grundlagen komplexere mathematische Sätze herzuleiten, ist ebenfalls kein rein theoretisches Konstrukt sondern aus ganz praktischer physikalischer Erfahrung gewachsen.
 „Wenn ich in den Pool springe (A), werde ich nass (B).“ ist eine logische Implikation. (A -> B, Dass ich in den Pool springe, ist also eine hinreichende (aber nicht notwendige) Bedingung dafür, dass ich nass werde.) Mit anderen Verknüpfungen der Aussagenlogik verhält es sich ähnlich. Sie sind Abstraktionen alltäglich erlebbarer physischer Phänomene.
„Wenn ich in den Pool springe (A), werde ich nass (B).“ ist eine logische Implikation. (A -> B, Dass ich in den Pool springe, ist also eine hinreichende (aber nicht notwendige) Bedingung dafür, dass ich nass werde.) Mit anderen Verknüpfungen der Aussagenlogik verhält es sich ähnlich. Sie sind Abstraktionen alltäglich erlebbarer physischer Phänomene.
Somit sind die Grundlagen wie auch das Werkzeug, mit dem man aus ihnen komplexere Sachen herleitet, empirisch begründete Vorstellungen davon, wie unser Universum so zu funktionieren scheint. Die daraus ziehbaren mathematischen Schlüsse funktionieren ebenfalls prima, um überprüfbare Naturgesetze zu formulieren. Wenn das nicht klappen würde, könnte ich das hier in dieser Form nicht schreiben, weil es gar nicht möglich wäre, Computer zu konstruieren. Alles, was du gerade um dich herum siehst, funktioniert übrigens ziemlicher sicher nur, weil die Naturgesetze immer und überall zuverlässig greifen, und der ganze Technik-Schnickschnack nur, weil irgendwer sie herausgefunden/verstanden hatte, und mit diesem Wissen den Ingenieuren erst die Möglichkeit gab, sinnvolle Sachen zu bauen. 🙂
Momentan denke ich also, dass wir es bei Mathematik und Logik in dem Maße mit Entdeckungen zu tun haben, wie das bei den Naturgesetzen auch der Fall ist. (Klar, man kann sagen, dass die Modellvorstellungen/Theorien, die man sich von irgendwelchen Phänomenen macht, erfunden sind, um diese zu erklären, aber du weißt vermutlich hoffentlich, was ich meine. ;)). Die tatsächlich bewiesene Richtigkeit eines Satzes innerhalb eines strukturwissenschaftlichen Systems ist unabhängig von dessen Ursprüngen trotzdem absolut wahr (und nicht nur wahrscheinlich nicht falsch), weil es dabei dann nur noch um die Konsistenz innerhalb dieses Systems geht. Grundlegende Entdeckungen können dann einen Kreislauf von Erfindung und Entdeckung anstoßen.
Warum unser Universum allerdings so mathematisch drauf ist, ist wieder eine andere Frage. Wenn es launischer wäre könnten wir jedoch vermutlich auch kaum solche komischen Fragen stellen. Oh, ist das Universum eigentlich ein INTJ? Informationen über sein inneres muss man ihm aufwendig aus der Nase ziehen (Introvertiert), es basiert auf wenigen abstrakten Prinzipien (iNtuitiv), es ist logisch (Thinking), und funktioniert zuverlässig (Judging). 😉
Natürlich beißt sich die Katze irgendwo selbst in den Schwanz wenn man Logik benutzt, um über die Wahrheit der Logik nachzudenken, allerdings funktioniert sie ja bekanntlich recht gut, was wir ja wissen, weil wir es empirisch (und damit logisch) überprüft haben. Oh, verdammt! 😀
Für mich fühlt sich dieser ganze Rekonstruktions-Kram nach der Postmodernen, irgendwie so an wie nach ’nem Sturm, der alles weggefegt hat, aus seinem Loch zu kommen und zu gucken, was übrig gelassen wurde und ob man mit dem, was man von früher kennt, irgendwas neues schönes bauen könnte. 😉




Pingback: Dogmen, Vernunft und Abrissbirnen | dem Dobi sein Blog
Meines Erachtens nach würde ich die Mathematik als Erfindung sehen.
Soweit ich das Verstanden habe, hängt die Konstruktion unserer Mathematik von unseren Erfahrungen mit unserer Umwelt ab, die wiederum beschränkt durch unsere rezeptiven Fähigkeiten ist. Wir sehen wie Welt funktioniert, kreieren axiomatische Systeme, hantieren mit ihnen herum und sehen, dass alle Ergebnisse innerhalb dieser Systeme sich wundervoll auf die Realtiät übertragen lassen. Dies funktioniert auch wunderbar, da es auf dem gründet was wir wahrnehmen. Nun, es ist aber nicht gesagt, dass dies wirklich die „Funktionsweise“ der Natur wiederspiegelt.
Stelle man sich als Beispiel die Werbung von dem Sony Xperia Handy vor, wo der kleine Junge behauptet im Handy würden Roboter arbeiten, die alles am Laufen halten. In seiner Vorstellung bzw. in seinem System könnte er somit das ganze Handy erklären. (Es wäre sogar sicher möglich ein paar Beweise in diesem System zu führen, sofern einiges als Vorausgesetzt gilt :D) Trotzdem ist es aber weit weg von der eigentlichen „Natur“ des Handys.
Ungefähr so stelle ich es mir mit der Mathematik vor. Es ist eine Erfindung, die aus unserer Wahrnehmung resultiert. Es ist möglich, dass sie schon exakt die Gesetze der Natur wiederspiegelt, aber mit 100%iger Sicherheit können wir das nicht sagen und werden es wohl auch nie sagen können. Denn der kleine Junge wird wahrscheinlich auch nicht wissen, dass seine Roboter kleine integrierte Schaltungen sind. Und selbst wenn er es irgendwann herausfindet, wird er immer noch nicht wissen, dass kleine Elektronen durch die Leitungen sausen. 🙂
Danke für den Kommentar so kurz vor deiner Mathe-Klausur. XD
Ja, ich denke ja auch nicht, dass es eine Entdeckung im Sinne von „mit 100%iger Sicherheit wahr“ ist, sondern wie die Naturgesetze eine Modellvorstellung für das, was wir (möglicherweise verfälscht) wahrnehmen, ist. Mir geht es hauptsächlich darum, die Trennung „Mathe ist Erfindung, Naturgesetze sind Entdeckungen.“, die man ja manchmal hört, aufzulösen, weil ich denke, die beiden tun sich da nicht wirklich soo viel. Wie man es dann letztendlich nennt, ist mir gar nicht so wichtig, solange man weiß, was damit gemeint ist. Ich hab mich dann nur für eine abgeschwächte Form des Worts „Entdeckung“ entschieden, weil ich es damit gegenüber „Der Geschichte von Hänsel und Gretel.“ und sowas absetzen wollte, und weil die Struktur des Universums die Modelle (Mathe und Naturgesetzte) irgendwie nahe legt und sie dadurch dann doch in gewisser Weise inhärent in ihm drin stecken. Ansonsten bliebe ja gar nichts mehr übrig, was man überhaupt „Entdeckung“ nennen könnte. 🙂
Pingback: Was machen Informatiker (bzw. Softwareentwickler im Speziellen) eigentlich so? | dem Dobi sein Blog
Pingback: Dinge, die wir eventuell gar nicht verstehen können | dem Dobi sein Blog