Wenn man angeborene Verhaltensweisen oder zumindest die genetische Komponente, die gewisse kulturell (Erziehung, Peers, Erlebnisse, Umwelt allgemein) hervorrufbare Ausprägungen begünstigt, nicht dadurch versucht zu erklären, dass sie jemand in uns hineingezaubert hat, sondern dadurch, dass diese Merkmale genauso durch Mutation und Selektion entstanden sind wie körperliche Eigenschaften auch, ist man im Bereich der evolutionären Psychologie angelangt. Hier bedient man sich gern der Spieltheorie (eine mathematische Disziplin, die sonst besonders in der Betriebswirtschaftslehre benutzt wird).

Ein klassisches abstraktes (Oft hilft es, komplexe Vorgänge zu vereinfachen, damit man überhaupt eine Möglichkeit zum Verstehen hat. Das konkrete Verhalten eines einzelnen Menschens in einer bestimmten Situation lässt sich dadurch selbstverständlich nicht zuverlässig vorhersagen.) Beispiel hier ist das prisoner’s dilemma (PD). Wie es zu seinem Namen kommt, ist hier jetzt egal. Das PD steht für Situationen, in denen zwei Individuen (nennen wir sie hier mal A und B) miteinander interagieren und dabei kooperieren (C) oder defektieren (betrügen/ausnutzen/nicht kooperieren) (D) können, sich jedoch für eins von beidem entscheiden müssen bevor sie wissen, was der jeweils andere macht. Das Ausdenken von entsprechenden Beispielen sei hier dem interessierten Leser selber überlassen. 😛
Je nachdem, wie sich A und B verhalten, haben sie dadurch unterschiedliche Vorteile/Nachteile (Geld, Prestige, Nahrung etc.).
Die entsprechende payoff matrix dazu sieht dann (mit den gleichen Beispielwerten wie hier) so aus:
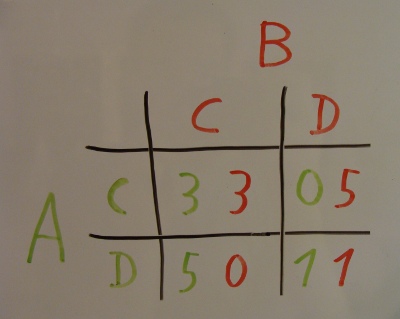In grün ist links die Aktion von Spieler A und in rot oben die Aktion von Spieler B eingetragen.
Wenn beide Spieler kooperieren (C,C) bekommen beide Spieler 3 Punkte.
Wenn Spieler A kooperiert, B aber nicht (C,D), dann erhält A 0 Punkte und B 5.
Wenn Spieler A defektiert, C aber kooperiert (D,C), dann erhält A 5 Punkte und B 0.
Wenn beide Spieler defektieren, erhalten beide nur einen Punkt.
Das bedeutet, dass es für beide Spieler zusammen als Team betrachtet am besten wäre wenn beide kooperieren würden. Dann würden insgesamt 6 Punkte verteilt. Bei einer einzelnen Spielrunde ist das allerdings kein Nash-Gleichgewicht.

Was bedeutet das?
Wenn ein Spieler kooperiert wäre es aus der Sicht des anderen besser, zu defektieren. Er würde ja 5 statt 3 Punkte (die er beim kooperieren bekäme) erhalten.
Wenn ein Spieler defektiert wäre es aus der Sicht des anderen besser, auch zu defektieren. Er würde dann ja 1 statt 0 Punkte (die er beim kooperieren bekäme) erhalten. Die best response ist also immer, nicht zu kooperieren, und hier die strikt dominante Strategie.

Joa, sieht ziemlich übel aus, oder? Nicht zu kooperieren ist das beste, um für sich selbst das Beste rauszuholen. Warum tut man das also nicht, sondern kooperiert mit anderen? Ein einfacher Fall ist der, dass man mit dem anderen verwandt ist. Nach Hamilton’s rule gibt es ja ein (auch in der Natur oft zu beobachtendes) Verhalten, was man mit Augenzwinkern kurz mit „Ich würde mein Leben für zwei Brüder oder 8 Cousins opfern.“ beschreiben kann. Das ergibt sich automatisch wenn man Selektion nicht aus Sicht der Individuen sondern deren Gene betrachtet. (Geschwister haben 50% der Gene gemeinsam, Cousins 12,5%.)

Man kooperiert ja aber auch mit Nichtverwandten. Warum?
Weil die Größen der Gruppen, in denen unsere Psyche evolvierte, so klein waren, dass man auf jedes andere Individuum mehrmals traf. Nun möchte man ganz abstrakt herausfinden, welche Strategie bei wiederholtem (Wie oft ist unbekannt. Das ist wichtig. Die Erklärung dafür würde allerdings den Rahmen hier sprengen.) langfristig die erfolgreichste ist.

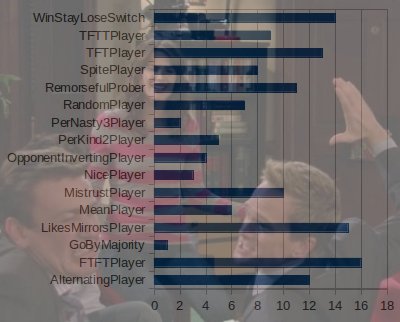
Dazu wurde in den 80er Jahren ein Computerturnier veranstaltet, bei dem verschiedene programmierte Strategien gegeneinander antreten mussten. Da es zu guter wissenschaftlicher Vorgehensweise gehört, Experimente zu wiederholen, um sie unabhängig zu überpfüfen (Bullshit, es hat mir einfach tierischen Spaß gemacht. :)) habe ich in Python 3 auch so ein Turnier implementiert. Den source code dazu habe ich hier hochgeladen: Zurück zur theoretischen Ebene: Da es zwischendurch auch zu Missverständnissen (man denkt, jemand hätte nicht kooperiert, obwohl er es hat) oder zu Versehen (jemand wollte kooperieren, ist aber gescheiert, und keiner hats bemerkt) kommen kann, ist es gut, noch einen Vergebungsfaktor in seine TFT-Strategie einzubauen (Forgiving Tit For Tat – FTFT). Ohne dieses gelegentliche Vergeben würden sich zwei normale kooperierende TFT-Spieler (C,C; C,C; C,C; …) nach nur einmal Defektieren auf immer und ewig gegenseitig das D heimzahlen (C,D; D,C; C,D; D,C). Eine solche Vendetta (Blutrache) wäre natürlich für beide beteiligten von Nachteil.
Zusätzlich zum (F)TFT bietet sich die Möglichkeit, Defektoren auch noch aktiv zu bestrafen. Dabei geht man selbst das Risiko ein, verletzt zu werden. Wenn nicht ist es zumindest Aufwand, den man auch für andere Sachen (die einem selbst direkt etwas bringen) hätte einsetzen können. So gesehen ist Rache also altruistisch (uneigennützig/selbstlos).

Gruppen, in denen solche Individuen, die sich aktiv rächen, vorhanden sind, sind durch Defektoren-Bestrafung geförderde Kooperation besser dran als Gruppen ohne. Auch bei großen Gruppengrößen kann dieses Verhalten stabil sein. (Die mathematische Herleitung gibt es hier: http://www.pnas.org/content/100/6/3531)
Mittlerweile haben wir natürlich ein Rechtssystem. Selbstjustiz ist oft nicht mehr erwünscht. Mal abgesehen davon, dass sich unsere Gene nicht in einer solchen Kultur entwickelt haben und viele davon ja auch schon in anderen Primaten vorhanden sind, gibt es jetzt ja auch noch Situationen im Alltag, die natürlich nicht rechtlich erfasst sind, und in denen wir ständig (F)TFT spielen.

Nach viel Blabla haben nun also Sätze wie „Das nächste mal kann die ihren Scheiss alleine machen.“ oder „Dem Asi verpass‘ ich ’ne verdiente Schelle.“ eine gute Begründung.

Ist es nicht schön, dass Kooperation und Vergebung nicht nur einfach nette, sondern auch mathematisch herleitbar nützliche Taktiken sind? 🙂

Außerdem wären die vielen tolle Kung-Fu-Filme ziemlich langweilig wenn unsere Belohnungszentren im Gehirn nicht darauf ansprechen würden, dass der Übeltäter mit roundhouse kicks ‚was auf die Nase bekommt. 😉