Es gibt keine Erfindungen, sondern nur Entdeckungen.

So, diese Aussage werde ich in diesem Artikel vertreten.

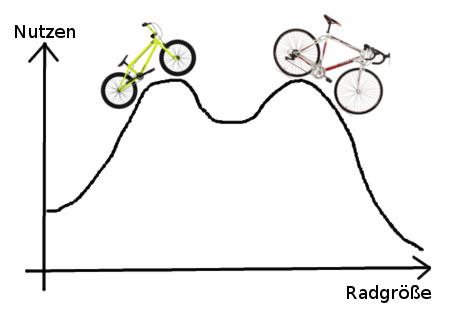
Angenommen du entwickelst Fahrräder. Du fängst zufällig mit etwas an, dessen Räder noch zu groß sind. Langsam benutzt du immer kleinere Räder, bis du ein für eine normale Körpergröße passendes Optimum gefunden hast. Etwas kleiner fährt sich schon nicht mehr so gut.

Leicht bekifft baust du aber irgendwann einfach aus Spaß mal eins mit wesentlich kleineren Rädern, und plötzlich bemerkst du, dass das doch gar nicht so schwachsinnig ist. Man kann zwar nicht so schnell damit fahren, aber viel bessere Stunts hinlegen. Hast du jetzt das BMX erfunden? Nein, du hast es nur entdeckt. Der Lösungsraum war nämlich schon lange vorher gegeben.

Du hast dich bisher jedoch einfach nur im rechten lokalen Optimum aufgehalten und dabei gar nicht gemerkt, dass es weiter links noch eins gibt.

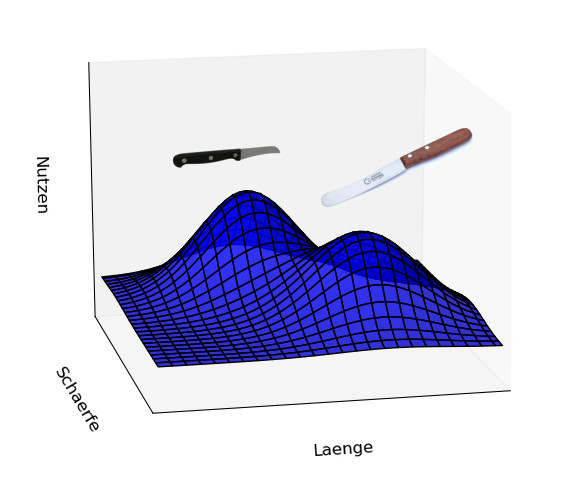
Wenn mehr als nur eine Grundeigenschaft eines Produkts oder einer Idee gleichzeitig verändert werden müssen, damit man ein neues Optimum findet, sieht das ähnlich aus. Ein Beispiel für eine Optimierung auf einem zweidimensionalen Lösungsraum ist die Herstellung von Messern. Wenn wir nur Frühstücksmesser und Obstmesser in Betracht ziehen, gibt es wieder zwei Nutzen-Optima; kurz und scharf sowie lang und weniger scharf.

Diese beiden Beispiele sind natürlich sehr stark vereinfacht. In Wirklichkeit haben die Lösungsräume, in denen wir uns bewegen, wesentlich mehr Dimensionen und sehen auch deutlich wilder aus. Das Prinzip in diesem Gedankenmodel bleibt jedoch das Selbe.

Gegeben ist ein Problem, für das eine möglichst gute Lösung gesucht wird. Dabei können sehr viele Parameter der Lösung variiert werden. Die Abhängigkeit des Nutzens von diesen extrem vielen Parameterkombinationen existiert jedoch bereits. Sie ist bisher jedoch nur in einem sehr kleinen Teil des Raums erkundet worden. Wenn wir eine gute Lösung „erfinden“, entdecken wir also lediglich eine sinnvolle Parameterkombination im gegebenen Lösungsraum.

Wenn wir auf der Suche nach einer neuen Lösung sind, ist die Aussicht aber nicht immer so super, dass man direkt sehen würde, wo der höchste Berg denn nun ist. Er könnte ja irgendwo außer Sichtweite sein. Wenn man auf so einen Berg gelangen will, reicht es natürlich nicht, von seiner Startposition aus einfach immer nur solange bergauf zu gehen, bis es nicht weiter hoch geht. So könnte man am Ende ja einfach auf einem kleinen Hügel stehen ohne zu bemerken, dass ganze Gebirgsketten irgendwo anders auf einen warten.
Zwar verändert sich die Landschaft ständig, und wenn man lange genug wartet, existiert vielleicht irgendwann tatsächlich ein stetig ansteigender Weg von unserer Startposition zum Supergipfel, jedoch würde es ziemlich lange dauern, bis es mal soweit ist.
(Ähnlich funktioniert übrigens Evolution, zumindest wenn man nur die ungeschlechtliche Vermehrung betrachtet. Mit sexueller Fortpflanzung ist ein stetig ansteigender Weg nicht unbedingt nötig, da durch die Rekombination zweier verschiedener Positionen mit Glück auch Berge, die komplett von Tälern umgeben sind, erreicht werden können. Das bedeutet aber noch lange nicht, dass man deshalb im globalen Maximum landet, dazu gibt es zu viele lokale Maxima. Also nein, wir Menschen sind vermutlich nicht das absolut Perfekte, der Mount Everest der Biologie. 😉 )

Um den Vorgang schneller zu gestalten, braucht man Ideen. Eine Idee ist dann einfach ein Gefühl (oder bei guter Intuition für den Lösungsraum auch eine feste Überzeugung), dass es „dort hinten im Nebel“ ziemlich weit nach oben geht.
Das kann natürlich klappen, aber auch daneben gehen. Die Kosten, um eine solche Lösung auszuprobieren, also einen unbekannten Teil des Lösungsraums zu erkunden, können selbstverständlich stark variieren, und werden meistens gegen den erwarteten Nutzen abgewogen.

Also, einfach mal auf Expedition gehen, und wenn ihr dann zufällig der erste auf einem vorher unbekannten Berg seid, lasst euch direkt den ganzen Kontinent patentieren, damit euch bloß keiner besuchen kommt. 😀